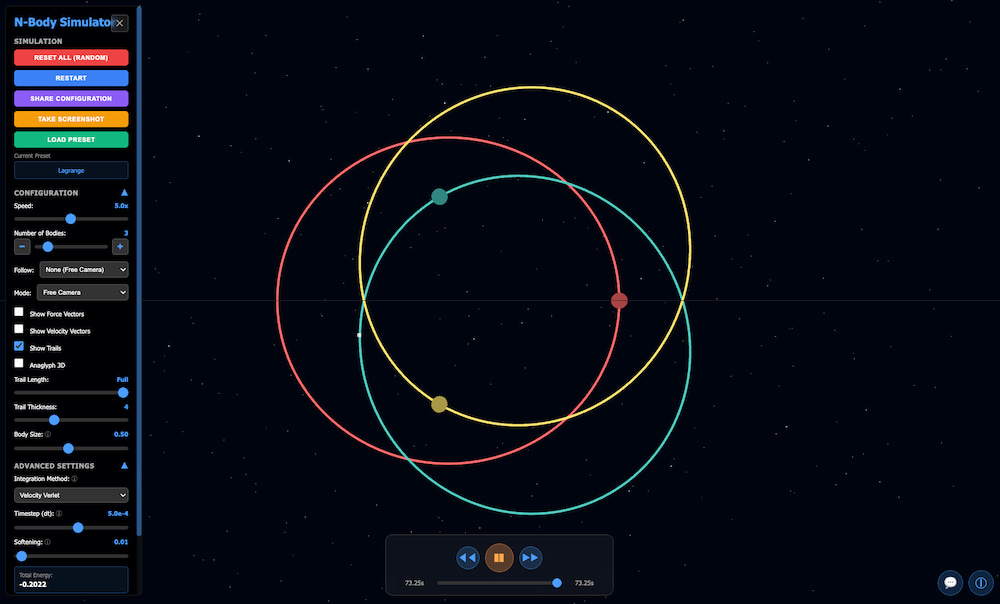
Bajo el dominio de TriSolar Chaos hay un estupendo simulador del problema de n-cuerpos en la física gravitacional. En su variante más conocida, el problema de los tres cuerpos ya es algo endiabladamente enrevesado; si se añaden más cuerpos celestes, imagina.
El problema de los tres cuerpos intenta prever el movimiento de tres masas que se atraen gravitatoriamente entre sí. Aunque cada par de cuerpos sigue la ley de gravitación universal de Newton, al interactuar los tres simultáneamente el sistema se vuelve caótico: pequeñas variaciones iniciales producen trayectorias muy distintas y no existe una solución general en forma cerrada. Solo pueden obtenerse soluciones numéricas o casos especiales con simetrías concretas, lo que lo convierte en uno de los problemas clásicos más complejos de la mecánica celeste.
En la simulación puede verse cómo son algunas de esas soluciones concretas que se conocen: una en forma de 8, descubierta en 1993, la de Lagrange en la que los tres cuerpos se configuran en una especie de triángulo de órbitas circulares y las de Hénon, Yark, Broucke u Suvakov-Dmitrasinovic (algunas con «rebotes» incluidos). Todas estas son configuraciones planas, por cierto.
Añadir más cuerpos es multiplicar la dificultad: esto es lo que se conoce como problema de los n cuerpos, que comenzaría con los casos de 2 y 3 cuerpos ya conocidos y seguiría con el de 4 cuerpos, que tampoco tiene soluciones analíticas pero del que se conocen también soluciones simétricas, periódicas y restringidas. Cuantos más cuerpos, más caos: con 5 y más cuerpos las soluciones «bonitas» son excepcionales y solo hay algunas muy especiales y simétricas. En el caso del Sistema Solar, por ejemplo (9 cuerpos) todo se resuelve mediante computación numérica, porque hay demasiadas variables, no es un problema integrable en general y no hay una solución universal.
Eso sí, cuando en mecánica orbital se trabaja con estos casos se aprende mucho sobre estabilidad, caos, resonancias, familias de órbitas periódicas, criterios de colisión y escape y otras cuestiones prácticas que resuelven el problema, no sin gran esfuerzo.
La página del simulador permite jugar con muchas opciones y además también permite visualizarlo todo en 3D, con diversos «puntos de cámara». De este modo puede verse cómo esas configuraciones estables en 3D, que son muchas menos que en 2D, tienen su interés y forman muchas veces órbitas en torno a tetraedros, bipirámides y prismas, algo realmente fascinante.
No hay que olvidar que en el MundoReal™ tenemos tres dimensiones espaciales, y que incluso en nuestro Sistema Solar, que tan «aplanado» nos parece, hay órbitas con inclinaciones entre 0 y 17° respecto a lo que sería un plano ideal.
Relacionado: