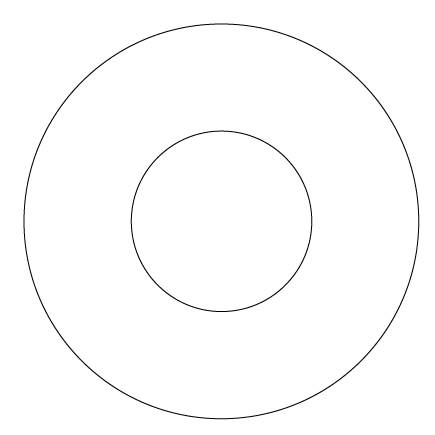
Cliff Pickover lanzaba la pregunta de si en dos círculos concéntricos, uno más grande y otro más pequeño, el círculo grande contiene más puntos que el círculo pequeño. Si se piensa un poco, se puede ver que es una pregunta que dista mucho de tener una respuesta directa e intuitiva. Más bien lleva a replantearse lo que George Cantor denominó los resultados contraintuitivos del infinito.
La solución correcta es que ambos círculos contienen los mismos puntos. Todos los círculos que existen contienen infinitos puntos, de modo que podría decirse que la respuesta correcta* sería una especie de «empate técnico»: el círculo grande contiene infinitos puntos y el pequeño contiene también infinitos puntos, de modo que ambos tienen la misma cantidad de puntos. (Matemáticamente: la misma cardinalidad).
Si esto recuerda a las paradojas de Cantor y Hilbert, como la del hotel infinito es porque algo tienen en común. Es una extensión del hecho de que un subconjunto puede tener la misma cantidad de elementos que el conjunto que lo contiene sin que nada se «rompa». En el intervalo entre (0,1) hay tantos puntos como en el (0,2), una recta infinita tiene tantos puntos como un segmento finito y el plano tiene tantos puntos como un cuadrado.
Si todo esto huele un poco a cuerno quemado es porque en el MundoReal™, más allá de los conceptos matemáticos, no estamos acostumbrados a esta forma de ver las cosas, incluso idealizándose. En la práctica medimos los círculos geométricamente y, suponiendo una distribución uniforme de los puntos, y dado que el área de círculo grande es mayor que la del círculo pequeño, concluimos que el grande contiene más puntos que el pequeño.
Pero vista la pregunta desde el punto de vista de la cardinalidad de la teoría de conjuntos, ambos tienen la misma: la del continuo (concretamente, «dos elevado a aleph cero»). El hecho de que el círculo pequeño esté contenido en el grande, o que obviamente haya más puntos fuera del círculo pequeños y razonamientos similares, no valen aquí. Grande o pequeño, ambos contienen la misma cantidad de puntos.
_____
* Disculpas por adelantado si hay errores, pero es que no soy matemático.
Relacionado:
- El paradójico hotel infinito de Hilbert explicado en un vídeo
- Curiosidades del infinito en el Hotel Infinito
- Historia del Infinito, uno de los más indescifrables conceptos
- ¿Cuán grande es el infinito?
- The Infinite Book
- Diez hechos matemáticos sorprendentes
- La escalera de infinitos escalones que parece medir 2 y √2
- Seis historias animadas que te harán pensar y aprender
- 1 – 2 + 3 – 4 + 5 – 6 + … = 0,25



